(Research) What causes the arctic amplification of surface warming?

The Earth's surface is warming 2-3x faster in the Arctic than the global average. There is still debate on which mechanism is dominant in generating Arctic amplification of surface air warming.

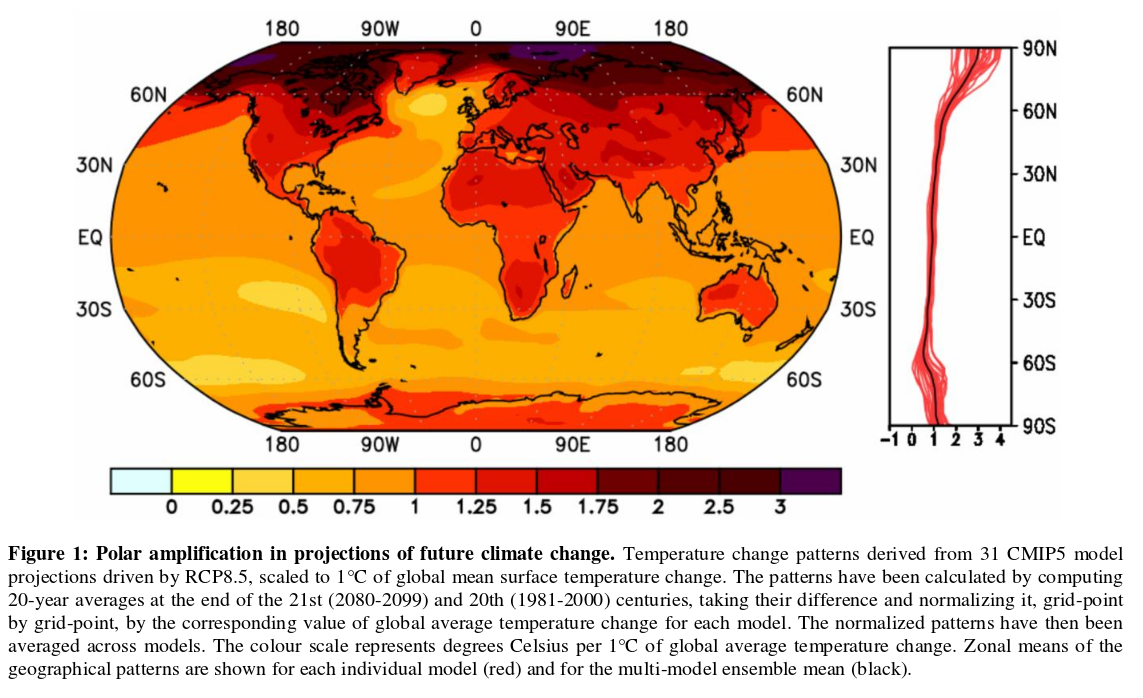
The figure above is from Smith et al. 2018 and shows the pattern of surface warming in projections of future climate change. The land warms faster than the ocean and the Arctic region warms from 2 to 4 times faster than the global mean $($see zonal average plot on the right$)$.

What are the possible reasons for this amplified warming?

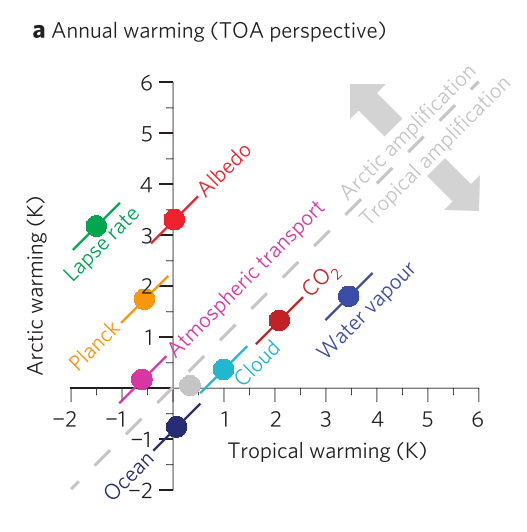
Using radiative kernels, Pithan and Mauritsen 2014 decomposed the pattern of warming into contributions from the different forcings and feedbacks. The figure above shows how much each forcing and feedback contribute to tropical warming $($x-axis$)$ and Arctic warming $($y-axis$)$. The albedo, for example, is a feedback that only affects the high latitudes, hence does not contribute to tropical warming $($0 on x-axis$)$ but does contribute to Arctic warming $($around 3.3K$)$. The distance from the one-to-one line $($gray dashed$)$ indicates whether the forcing/feedback contributes to Arctic or tropical amplification.

There are problems with this accounting method as there is significant interaction between each process. For example, keeping the surface albedo feedback fixed would increase the role of atmospheric energy transport in amplifying Arctic warming, so this attribution method may be misleading $($see Merlis $(2014)$$)$. Our method for analysing the importance of each of these processes is to use idealized climate models to gain a physical understanding on how they lead to Arctic amplification.

Sea ice albedo feedback

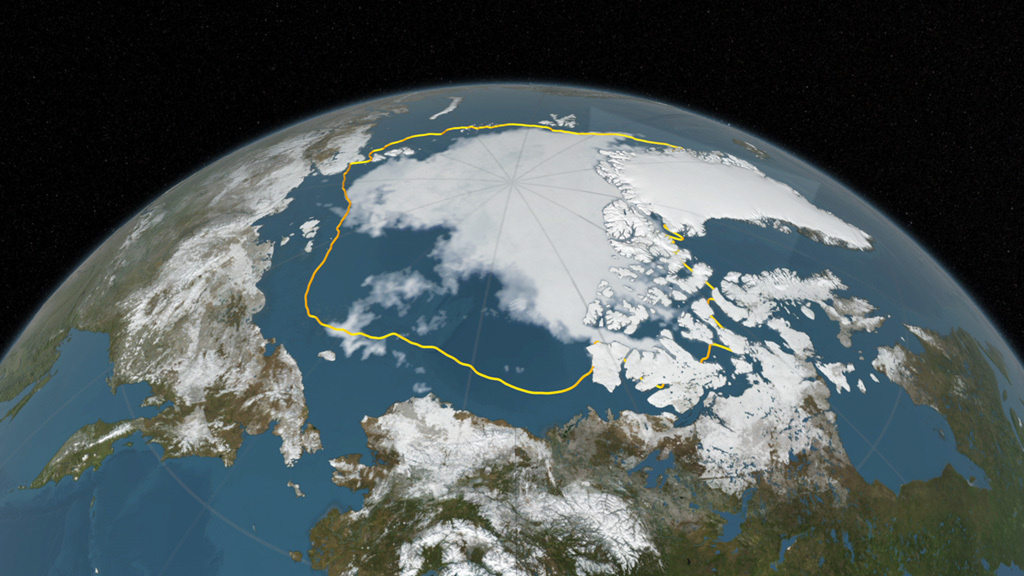
This figure from NASA shows the 2016 Arctic sea ice minimum $($911,000 square miles$)$ and the 1981-2010 average $($gold line$)$. This decrease in sea ice extent leads to a decrease in surface albedo and induces additional local warming.

As can be seen from the Pithan and Mauritsen $($2014$)$ figure, this is one of the dominant mechanisms for Arctic amplification. However, idealized climate models that keep the surface albedo fixed as the climate warms or have no sea ice at all still have polar amplification. $($The amount of polar amplification in these simulations depends on the type of insolation used $($see Kim et al. $($2018$)$$)$.$)$ This suggests there are more fundamental mechanisms at play.

Planck feedback

The instantaneous impact of increasing greenhouse gas concentrations is to reduce the outgoing longwave radiation $($OLR$)$ at the top-of-atmosphere $($TOA$)$. Since the global-mean TOA OLR must be equal to the absorbed solar radiation, which we assume does not change, the surface and troposphere must warm to increase the OLR. We artificially separate the vertical structure of warming into a vertically homogeneous part and its deviation. The Planck feedback corresponds to the total increase in OLR per degree of vertically homogeneous warming.

The OLR can be calculated as $OLR=\sigma T_E^4$, where $T_E$ is the temperature of emission. Since $\sigma T^4$ is nonlinear, a cold body needs a higher increase in temperature to reach the same increase in emitted radiation than a warm body. The high latitudes are colder than the rest of the planet, hence this is thought to be a cause for polar amplification. Moreover, Pithan and Mauritsen's figure shows that the Planck feedback may have an important part to play in Arctic amplification.

My first PhD project consisted in testing how important this mechanism is for polar amplification. We used an idealized atmospheric gray radiation model with aquaplanet surface boundary condition $($no continents$)$, no clouds and no sea ice $($Frierson et al. $($2006$)$$)$. We simply replaced $E=\sigma T^4$ by $E=A + BT$ in the radiation code so that the increase in temperature necessary to increase the OLR is the same for all initial temperatures. This had no effect on the pattern of surface air warming as other factors such as the lapse rate feedback changed to compensate. However, we did find that the $E=\sigma T^4$ nonlinearity affects the vertical structure of warming.

Atmospheric energy transport

While the role of the atmospheric energy transport does not seem dominant in Pithan and Mauritsen's figure, its role becomes important if the surface albedo feedback is artificially cancelled in idealized climate model simulations.

The simplest model to understand the role of atmospheric energy transport in polar amplification is the moist energy balance model $($see Hwang and Frierson $($2010$)$ for example$)$. In this one-dimensional model energy balance model, the difference between absorbed shortwave radiation and emitted longwave radiation is balanced by diffusion of moist static energy $($MSE$)$. Since saturation vapor pressure is exponentially related to temperature, the initial increase in temperature from a given forcing increases the water vapor content more in the tropics than in the poles. This increases the gradient of the moist component of the moist static energy, which leads to more convergence of moist static energy flux at high latitudes and amplified polar warming. Tim and I wrote a paper producing an estimate for polar amplification using this model which does not require the use of numerical model simulations.

Lapse rate feedback

The lapse rate feedback refers to the vertical structure of temperature change. A positive $($bottom-heavy$)$ lapse rate change leads to less outgoing longwave radiation change, whereas a negative $($top-heavy$)$ lapse rate change leads to more outgoing longwave radiation change relative to a vertically uniform temperature change. Hence, a positive lapse rate change is a positive $($destabilizing$)$ feedback and a negative lapse rate change is a negative $($stabilizing$)$ feedback.

According to Pithan and Mauritsen's figure, the lapse rate feedback contributes a lot to polar amplification. However, it is not clear that the lapse rate feedback refers to one specific physical mechanism. Cronin and Jansen $($2016$)$ propose an analytic radiative-advective model of the high latitude atmosphere, which shows that the lapse rate response depends on the forcing applied to the high latitudes. For example, a surface forcing would lead to a more bottom-heavy warming than an increase in atmospheric energy transport convergence. While their model is very idealized, this effect can be seen in Feldl et al.'s $($2017$)$ aquaplanet simulations, where the strength of the surface albedo feedback is varied. In the simulations with strong surface albedo feedback, there is little increase in atmospheric energy transport convergence and a strong increase in surface forcing due to the change in surface albedo, leading to a positive lapse rate change. However, in simulations with weak surface albedo feedback, there is little increase in surface forcing and a large increase in atmospheric energy transport convergence, leading to a negative lapse rate change.

This forcing dependence is specific to the high latitudes where the atmosphere is close to radiative-advective balance: the heating from atmospheric energy transport convergence is balanced by radiative cooling. However the tropics are close to radiative-convective equilibrium: the whole troposphere's temperature structure follows the moist adiabat and is determined by the surface temperature and relative humidity. The fact that high latitudes are in radiative-advective equilibrium might be the reason the Arctic amplified temperature change pattern is so robust.

Conclusion

A simple picture of the interaction between surface albedo feedback $($local$)$ and atmospheric energy transport $($remote$)$ processes in generating Arctic amplification can be deduced from Feldl et al.'s $($2017$)$ experiments. When the surface albedo feedback is strong, polar amplification is strong, the lapse rate change is very positive and there is no increase in atmospheric energy transport convergence: polar amplification appears to be a local phenomenon. However, when the surface albedo feedback is turned off, there is little to no polar amplification, the lapse rate feedback is negative and there is a high increase in atmospheric energy transport. This is consistent with Stuecker et al.'s $($2018$)$'s experiments that diagnose polar amplification to come mainly from local phenomena in GCMs that include surface albedo feedback. The presence of clouds in simulations with no surface albedo feedback may lead to a negative local cloud feedback in high latitudes and mask the polar amplified pattern of temperature change $($see Kim et al. $($2018$)$ for example in which fixed clouds simulations are compared to active cloud feedback simulations$)$. An aspect of Arctic amplification that is neglected here is its seasonality: Screen et al. $($2012$)$ show that Arctic amplification is mainly a winter phenomenon.